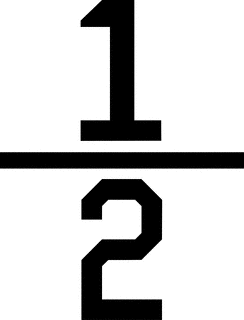Penambahan Pecahan
1. Cara menambah pecahan wajar yang mempunyai penyebut yang sama.
Contoh: 1/4 + 2/4 = 3/4
Bagi pecahan wajar yang penyebutnya sama kita hanya perlu menambah pengangkanya sahaja. Jangan ditambah penyebutnya. Kesilapan banyak dilakukan oleh pelajar dengan menambah kesemua pengangka dan penyebutnya.
Cara Begini Salah : 1/4 + 2/4 = 3/8
2. Cara menambah pecahan wajar apabila satu daripada penyebutnya adalah gandaan penyebut yang lain.
Contoh:
2/3 + 1/6 = 2 / 3 X 2/ 2 + 1/6
= 4/6 + 1/6
= 5/6
Tukarkan pecahan 2/3 kepada pecahan per enam dengan mendarab pengangka dan penyebutnya dengan 2.
Kesilapan yang biasa dilakukan oleh pelajar ialah dengan mencampur pengangka dan penyebutnya sekali gus.
Cara Begini Salah : 2/3 + 1/6 = 3/9
3. Cara menambah pecahan wajar apabila penyebutnya tidak ada faktor sepunya.
2/3 + 3/5 = 2/3 X 5/5 + 3/3 X 3/5
= 10/15 + 9/15
=19/15
= 1 4/15
4. Pelajar juga boleh menyelesaikan masalah operasi tambah tiga pecahan seperti berikut:
(a). Menambah tiga
pecahan wajar yang penyebutnya sama.
Contoh:
1/8 + 3/8 + 5/8 = 1/8 + 3/8 + 5/8
= 9/8 ( JANGAN LUPA MENUKAR PECAHAN TAK WAJAR KEPADA NOMBOR BERCAMPUR)
= 1 1/8
(b). Pelajar juga boleh
menambah tiga pecahan yang penyebutnya
tidak sama.
Contoh:
Contoh yang melibatkan pecahan
Sebuah pecahan
adalah sebahagian daripada keseluruhan.
satu per dua @ one-half
satu per empat @ one-quarter
tiga per lapan @ three-eighths
lihat contoh di bawah:
nombor
bercampur + nombor bulat
Sekiranya nombor bercampur ditambah dengan nombor bulat, maka;
TAMBAH NOMBOR BULAT terlebih dahulu.
Perbezaan di antara pecahan wajar, pecahan tidak wajar dan pecahan bercampur
Mari kita lihat apakah perbezaan antara ketiga-tiga jenis pecahan ini.
contohnya:
1) Pecahan wajar = hasil bahagi/ nombor pecahan < 1
2) Pecahan tidak wajar = hasil bahagi/nobor pecahan > 1
manakala, pecahan bercampur adalah paling mudah dikenalpasti apabila nombor bulat beserta pecahan digabungkan bersama.
Untuk kefahaman yang lebih jelas, kita boleh bezakan antara pecahan wajar dan tidak wajar berdasarkan nilai dalam bentuk perpuluhan.
contohnya:
1) Pecahan wajar = hasil bahagi/ nombor pecahan < 1
2) Pecahan tidak wajar = hasil bahagi/nobor pecahan > 1
manakala, pecahan bercampur adalah paling mudah dikenalpasti apabila nombor bulat beserta pecahan digabungkan bersama.
Jenis-jenis pecahan
terdapat 3 jenis PECAHAN iaitu:
ü pecahan wajar (proper fraction)
ü pecahan tidak wajar (improper fraction)
ü pecahan bercampur (mixed fraction)
Bahagian-bahagian pada pecahan
1 ---> pengangka / numerator
2 ---> penyebut / denominator
Tips:
Untuk mengingat nama bagi
setiap pengangka dan penyebut, guru bolehlah
tekankan bahawa peng‘A’ngka
iaitu A=atas dan angka adalah number dalam BI lalu diingati sebagai numerator.
Bagi penyebut pula, guru
boleh gunakan penye‘B’ut iaitu B=Bawah atau ‘D’enominator iaitu D=Down.
Pecahan / Fractions
Apa itu pecahan?
v
Pecahan ialah nombor yang mewakili
sebahagian daripada keseluruhan.
v
Nombor 1 mewakili semua bahagian dalam
keseluruhan.
v
Nombor 1 boleh diwakili oleh pecahan di
mana pengangka dan penyebutnya adalah sama.
Contoh: 2/2 , 4/4 , 6/6 =
1
Teknik Belajar Matematik
Ada beberapa perkara yang belajar daripada Budiyamin tentang matematik. Satu, kalau nak pandai matematik, kita kena suka matapelajaran tu. Habis, kalau kita dah memang tak suka macam mana? Caranya, mula-mula buat-buat macam kita sukakan matapelajaran tu. Kita macam berlakon sikit yang kita suka subjek tu. Kemudian, mula buat latihan sedikit demi sedikit. Tak perlu terus mula dengan 100 soalan. Bukan apa, takut terkejut nanti lepas tu terus makin benci.
Kedua, matematik adalah latihan dan latihan adalah matematik. Maksud cikgu, matematik adalah satu subjek yang anda perlu buat latihan untuk menguasainya, bukan membaca. (Ada pelajar yang belajar matematik dengan hanya membacanya). Cikgu berjaya menguasai matematik kerana saya ikut Budiyamin buat latihan. Semakin banyak latihan saya buat, saya jadi semakin cekap. Malah, ramai kawan sekelas akan tanya cikgu dan Budiyamin tentang cara menjawab soalan matematik.
Ketiga, matematik adalah matapelajaran yang memerlukan disiplin. Walaupun anda faham topik tertentu, anda tidak akan dapat menjawab dalam masa yang diberikan jika anda tidak mendisiplinkan diri untuk menjawab soalan matematik. Setiap kali anda berlatih menjawab soalan matematik, catat masa yang anda ambil. Selalunya anda ada masa kurang daripada 3 minit untuk menjawab satu soalan. Jadi, cuba kejar masa itu, maksud cikgu, cuba latih menjawab dengan secepat mungkin.
Keempat, anda perlu HAFAL SIFIR! Saya tahu ramai pelajar yang merungut tentang perkara ini. Ada pelajar tingkatan lima yang saya uji dengan sifir 7 pun tidak lepas. Alasan mereka, mereka boleh guna mesin kira, mengapa perlu ingat sifir?
Persoalannya ialah, hafal sifir bukan sahaja untuk mengetahui berapa 5 x 5 dan berapa 12 x 7. Tetapi, menghafal sifir akan membuat otak anda lebih cepat dan cekap mengira. Kalau asyik bergantung kepada mesin kira, daya pemikiran anda akan semakin lemah kerana tidak ada usaha yang dilakukan oleh otak anda. Lihat mereka yang handal matematik, pasti mereka cekap juga dalam sifir.
Akhir sekali, anda perlu ada azam dan kemahuan untuk jadi hebat dalam subjek matematik. Semoga kalian berjaya.
